Improved Bubble Sort

Almost every developer know how to implement the bubble sort for a simple array. We just need to travel over the array in two levels and swap the adjacent elements in the second level if their values’ order is not correct.
The algorithm implement with Python is in the following code snippet. We arrange that the result order is ascending.

def bubble_sort(_array):
    for i in range(len(_array)):
        for j in range(len(_array) - 1, i, -1):
            if _array[j] < _array[j - 1]:
                _array[j], _array[j - 1] = _array[j - 1], _array[j]
    return _array

The above algorithm implementation moves the right to left as our expect order, it ensures that the left element is always less than the right element.

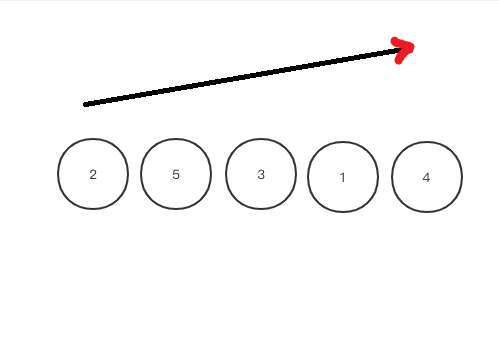
We will get the following result after every reorder based on the basic bubble sort.

[1, 2, 5, 3, 4]
[1, 2, 3, 5, 4]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 5]
[1, 2, 3, 4, 5]

We can get a clearer workflow by dynamic illustrating which is created by tool Wolfram Mathematica.

data={{1,2,5,3,4},{1,2,3,5,4},{1,2,3,4,5},{1,2,3,4,5},{1,2,3,4,5}}
Manipulate[BarChart[ data[[ a ]] ],{a,1,5,1}]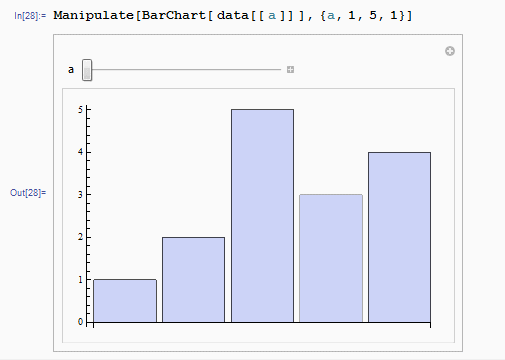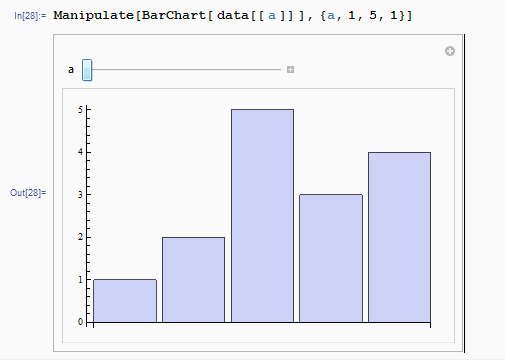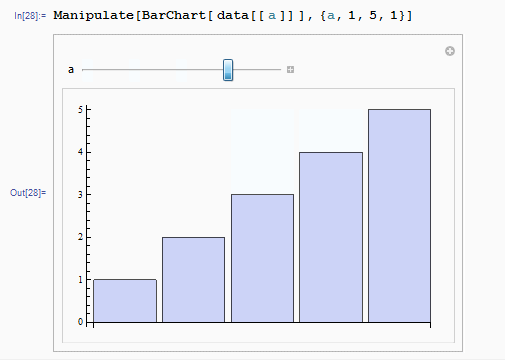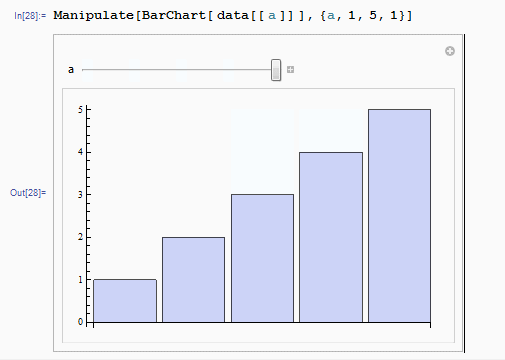

Actually the second level nth traversing will find the nth smallest element in the array and put it in the left position if we can’t find one, it means the nth element is the nth smallest element and rest elements in the right section are in restrict ascending order. The second level traversing is interesting, it doesn’t sort the rest elements completely but it can distinguish the sub-array which is not restricted ascending. So we can jump out from the loop and output result.

def improved_bubble_sort(_array):
    for i in range(len(_array)):
        stop = True
        for j in range(len(_array) - 1, i, -1):
            if _array[j] < _array[j - 1]:
                stop = False
                _array[j], _array[j - 1] = _array[j - 1], _array[j]
        if stop:
            return _array
    return _array