Use Local Coordinate System And Show It

How to create a local coordinate system and show it? We define the local coordinate system has its own x-axis, y-axis, z-axis, and origin.

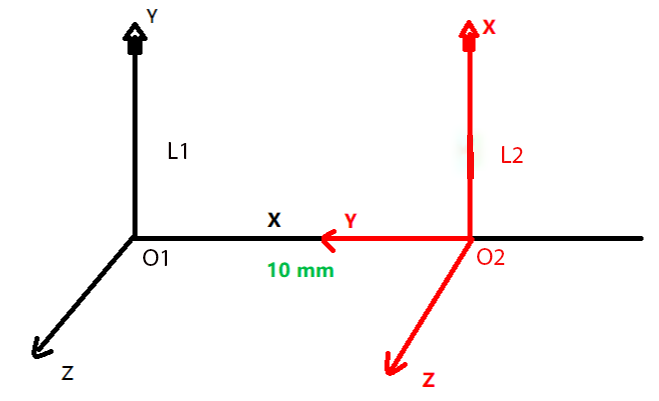
We call the left coordinate system L1 and the right coordinate system L2.
Regard L1 as the world coordinate system in VTK, the other one L2 is a local coordinate system.
Define a vector W.

We want to know the new expression V in the coordinate system L2.
Create a matrix transformation equation.

The matrix T can help us to convert W to the new expression in the coordinate system L2, we call T local coordinate matrix.
How to show the local coordinate system if we don’t know its status before?
The question is equal to compute the expression of E that a unit vector in L2 in the world coordinate system.
So we have the following equation.

We can apply the to a vtkAxesActor object to show the local coordinate system.
Let’s call the matrix pose coordinate matrix.

vtkSmartPointer<vtkTransform> CreateLocalTrans(PointStruct origin, PointStruct xDir, PointStruct yDir)
{
    vtkSPtrNew( resultTrans, vtkTransform );
    PointStruct zDir = xDir ^ yDir;
    zDir.Unit();

    double elements1[16] = { xDir[0], xDir[1], xDir[2], 0,
                            yDir[0], yDir[1], yDir[2], 0,
                            zDir[0], zDir[1], zDir[2], 0,
                            0, 0, 0, 1 };

    resultTrans->Concatenate(elements1);     //rotation

    double elements2[16] = { 1, 0, 0, -origin[0],
                             0, 1, 0, -origin[1],
                             0, 0, 1, -origin[2],
                             0, 0, 0, 1 };

    resultTrans->Concatenate(elements2);    //translation
    resultTrans->Update();

    return resultTrans;
}

int main()
{
    vtkSmartPointer<vtkTransform> local1  =
            CreateLocalTrans( PointStruct(0, 0, 0), PointStruct(1, 0, 0), PointStruct(0, 1, 0) );
    vtkSmartPointer<vtkTransform> local2  =
            CreateLocalTrans( PointStruct(10, 0, 0), PointStruct(0, 1, 0), PointStruct(-1, 0, 0) );

    vtkSPtrNew(m1, vtkMatrix4x4);
    m1->DeepCopy( local1->GetMatrix() );
    vtkSPtrNew(m2, vtkMatrix4x4);
    m2->DeepCopy( local2->GetMatrix() );
    m1->Invert();
    vtkSPtrNew(T, vtkMatrix4x4);
    vtkMatrix4x4::Multiply4x4( m2, m1, T );
    T->Print( std::cout );
    vtkSPtrNew(TTrans, vtkTransform);
    TTrans->SetMatrix( T );
    TTrans->Inverse();

    vtkSmartPointer<vtkAxesActor> axesActor =
            vtkSmartPointer<vtkAxesActor>::New();
    axesActor->SetUserTransform( TTrans );

    vtkSmartPointer<vtkRenderer> renderer =
            vtkSmartPointer<vtkRenderer>::New();
    renderer->AddActor( axesActor );
    renderer->SetBackground( 0, 0, 0 );

    vtkSmartPointer<vtkRenderWindow> renderWindow =
            vtkSmartPointer<vtkRenderWindow>::New();
    renderWindow->AddRenderer( renderer );

    vtkSmartPointer<vtkRenderWindowInteractor> renderWindowInteractor =
            vtkSmartPointer<vtkRenderWindowInteractor>::New();
    renderWindowInteractor->SetRenderWindow( renderWindow );

    renderer->ResetCamera();
    renderWindow->Render();
    renderWindowInteractor->Start();

Now let’s regard L1 as a local coordinate system and explore the transform matrix A.

means the new expression of W in the local coordinate system .
There is a transform matrix A that can help us to describe a vector or point in by system .
We can calculate the value of and apply it.

Split the matrix to rotate matrix and translate matrix.
Rotate matrix:

Translate vector:

We can find that the translate vector starts from system to system , it is described by system because we rotate firstly, and then move it to get the system .