CGAL: Useful Properties Of Matrix

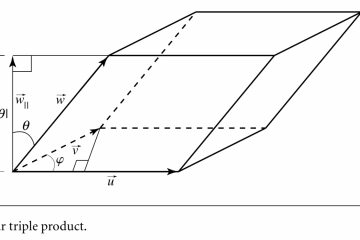
A(B+C) = AB + AC

We defined three different matrix A(m x n), B(n x r), and C(n x r), they satisfy distributivity of multiplication over addtion: A(B+C) = AB + AC.

#include <CGAL/Linear_algebraHd.h>
#include <CGAL/Linear_algebraCd.h>
#include <iostream>

using namespace std;
using namespace CGAL::Linear_Algebra;

typedef CGAL::Linear_algebraCd<double> LA;
typedef LA::Matrix Matrix;
typedef LA::Vector Vector;

template <typename Type>
Matrix BuildMatrix( int rowCount, int colCount, Type *values )
{
    std::vector<Vector> elements;
    for( int i = 0; i < rowCount; ++i ){
        std::vector<Type> tmp;
        for( int j = 0; j < colCount; ++j ){
            tmp.push_back( values[i*colCount + j] );
        }
        elements.push_back( Vector( tmp.begin(), tmp.end() ) );
    }
    Matrix M( elements.begin(), elements.end() );
    return M;
}

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );

    double values0[16] = { 1, 1, 2, 3, // column vector
                          0, 1, 0, 3,
                          0, 2, 5, 1,
                          0, 0, 10, 9 };
    auto A = BuildMatrix( 4, 4, values0 );

    double values1[16] = { 1, 0, 0, 3, // column vector
                           0, 1, 0, 0,
                           0, 0, 5, 1,
                           3, 0, 0, 0 };
    auto B = BuildMatrix( 4, 4, values1 );

    double values2[16] = { 1, 0, 0, 2, // column vector
                           0, 1, 0, 11,
                           2, 0, 2, 0,
                           0, 0, 0, 4 };
    auto C = BuildMatrix( 4, 4, values2 );

    auto tmp = A*(B+C);
    cout << tmp << endl;
    tmp = A*B + A*C;
    cout << tmp << endl;
    return 0;
}

Output:

LA::Matrix((4, 4 [2, 0, 2, 3,
2, 2, 16, 3,
54, 110, 49, 46,
51, 105, 22, 45,
])
LA::Matrix((4, 4 [2, 0, 2, 3,
2, 2, 16, 3,
54, 110, 49, 46,
51, 105, 22, 45,
])

The transposition of a matrix product

The transposition of a matrix product is equivalent to the product of the thransposition of every matrix, with the order of multiplication reversed.

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );

    double values0[16] = { 1, 1, 2, 3, // column vector
                          0, 1, 0, 3,
                          0, 2, 5, 1,
                          0, 0, 10, 9 };
    auto A = BuildMatrix( 4, 4, values0 );

    double values1[16] = { 1, 0, 0, 3, // column vector
                           0, 1, 0, 0,
                           0, 0, 5, 1,
                           3, 0, 0, 0 };
    auto B = BuildMatrix( 4, 4, values1 );

    auto result = LA::transpose( A*B );
    cout << result << endl;

    result = LA::transpose( B ) * LA::transpose( A );
    cout << result << endl;
    return 0;
}

Output:

LA::Matrix((4, 4 [1, 1, 32, 30,
0, 1, 0, 3,
0, 10, 35, 14,
3, 3, 6, 9,
])
LA::Matrix((4, 4 [1, 1, 32, 30,
0, 1, 0, 3,
0, 10, 35, 14,
3, 3, 6, 9,
])

The inverse of the matrix product

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );

    double values0[16] = { 1, 1, 2, 3, // column vector
                          0, 1, 0, 3,
                          0, 2, 5, 1,
                          0, 0, 10, 9 };
    auto A = BuildMatrix( 4, 4, values0 );

    double values1[16] = { 1, 0, 0, 3, // column vector
                           0, 1, 0, 0,
                           0, 0, 5, 1,
                           3, 0, 0, 0 };
    auto B = BuildMatrix( 4, 4, values1 );

    double det;
    auto result = LA::inverse( A*B, det );
    cout << result << endl;
    cout << "det: " << det << endl;

    result = LA::inverse( B, det ) * LA::inverse( A, det );
    cout << result << endl;
    cout << "det: " << det << endl;
    return 0;
}

Output:

LA::Matrix((4, 4 [-0.0224561, -0.0736842, 0.0112281, 0.0245614,
-0.621053, 0.368421, -0.189474, 0.210526,
-0.0378947, 0.0631579, 0.0189474, -0.0210526,
0.340819, 0.0245614, -0.00374269, -0.00818713,
])
det: 1
LA::Matrix((4, 4 [-0.0224561, -0.0736842, 0.0112281, 0.0245614,
-0.621053, 0.368421, -0.189474, 0.210526,
-0.0378947, 0.0631579, 0.0189474, -0.0210526,
0.340819, 0.0245614, -0.00374269, -0.00818713,
])
det: 1

Inverse the product of a number and a matrix

(with a != 0)

int main()
{
    CGAL::set_mode( cout, CGAL::IO::PRETTY );

    double values0[16] = { 1, 1, 2, 3, // column vector
                          0, 1, 0, 3,
                          0, 2, 5, 1,
                          0, 0, 10, 9 };
    auto A = BuildMatrix( 4, 4, values0 );

    double a = 10, det;
    auto result = LA::inverse( a*A,det );
    cout << result << endl;

    result = (1/a) * LA::inverse(A, det);
    cout << result << endl;
    return 0;
}

Output:

LA::Matrix((4, 4 [0.1, 0, 0, 0,
-0.0621053, 0.0368421, -0.0189474, 0.0210526,
-0.0189474, 0.0315789, 0.00947368, -0.0105263,
-0.0105263, -0.0157895, 0.00526316, 0.00526316,
])
LA::Matrix((4, 4 [0.1, 0, 0, 0,
-0.0621053, 0.0368421, -0.0189474, 0.0210526,
-0.0189474, 0.0315789, 0.00947368, -0.0105263,
-0.0105263, -0.0157895, 0.00526316, 0.00526316,
])