Here is a convex object and an origin point outside it.
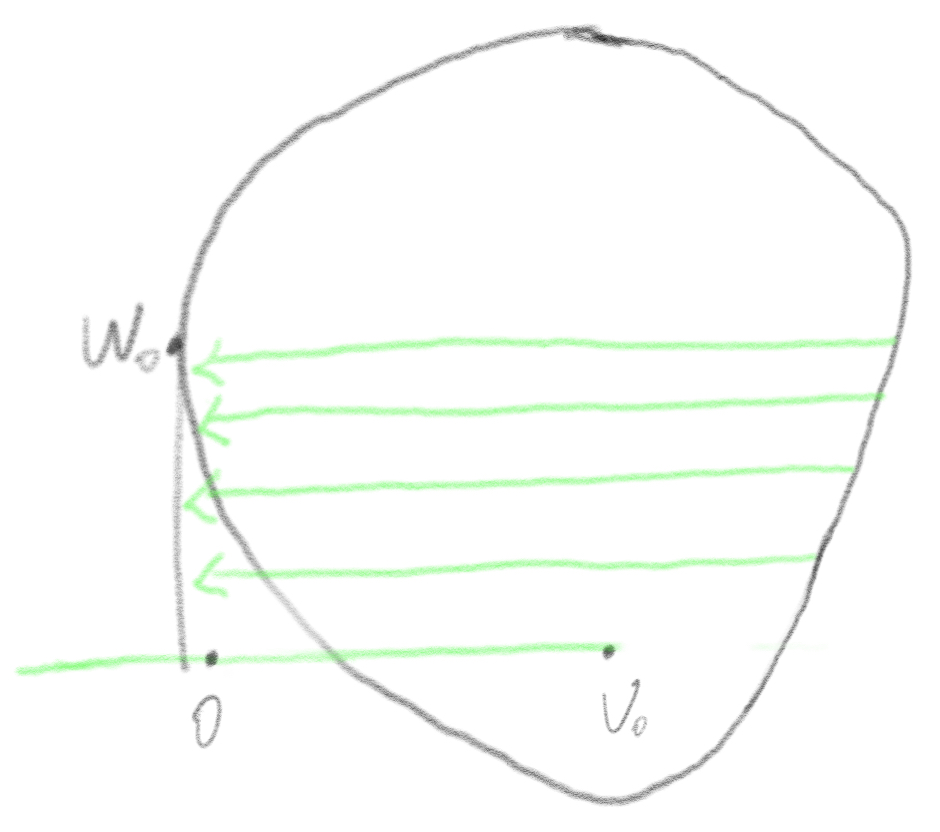
![]() is an arbitrary point in the boundary. Find the farthest point on the boundary along the vector
is an arbitrary point in the boundary. Find the farthest point on the boundary along the vector ![]() . Name the farthest point
. Name the farthest point ![]() .
.
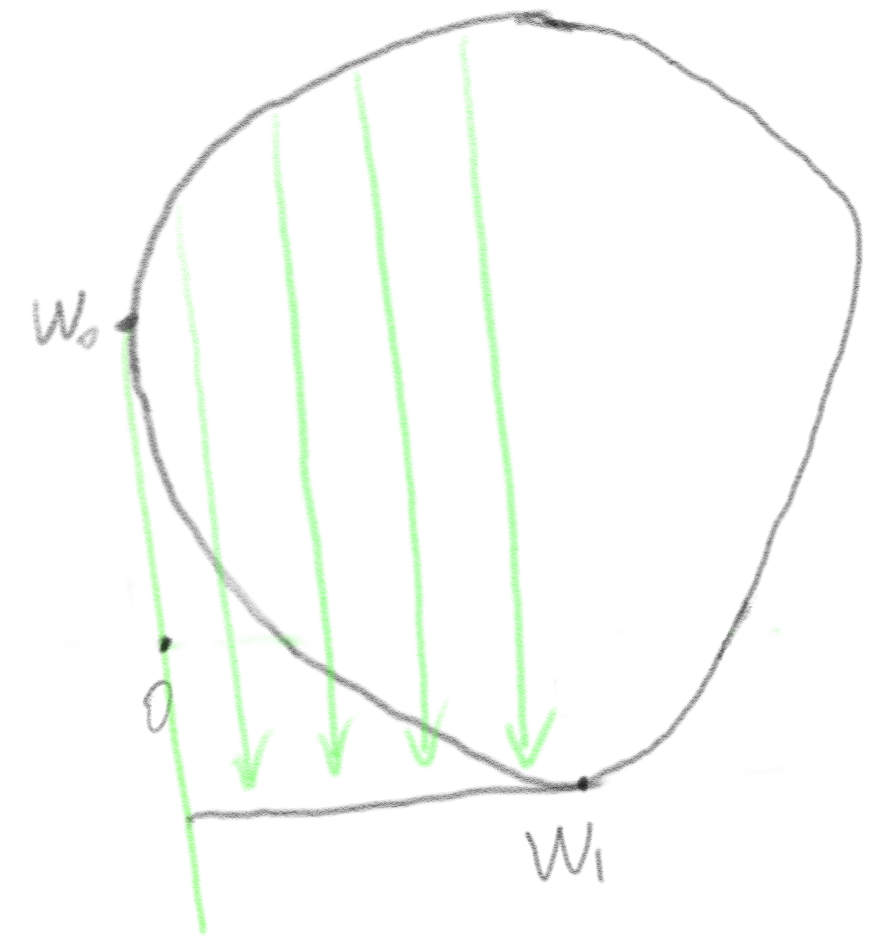
We get a new vector ![]() to find the farthest point on the boundary along the direction
to find the farthest point on the boundary along the direction ![]() . The point
. The point ![]() is added to the simple vertices set
is added to the simple vertices set ![]() = {
= {![]() ,
, ![]() }.
}.
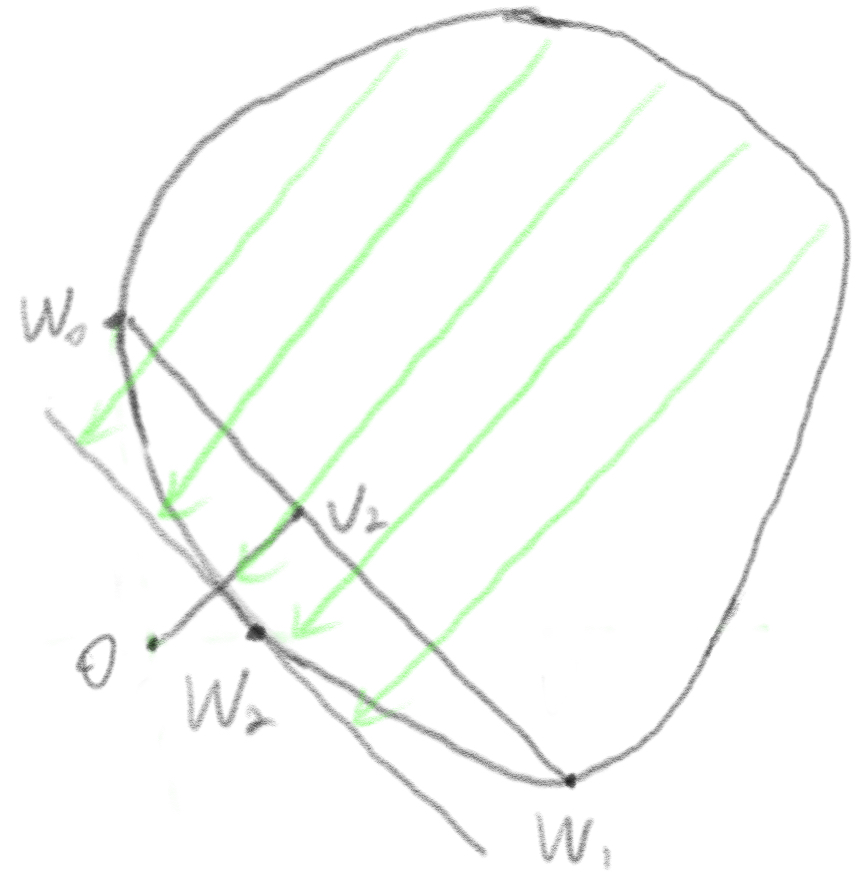
Connect points ![]() and
and ![]() , find the closet point
, find the closet point ![]() on the line segment to the origin O. Find the farthest point
on the line segment to the origin O. Find the farthest point ![]() on the boundary with direction
on the boundary with direction ![]() . The point
. The point ![]() is added to the simple vertices set
is added to the simple vertices set ![]() = {
= {![]() ,
, ![]() ,
, ![]() }.
}.
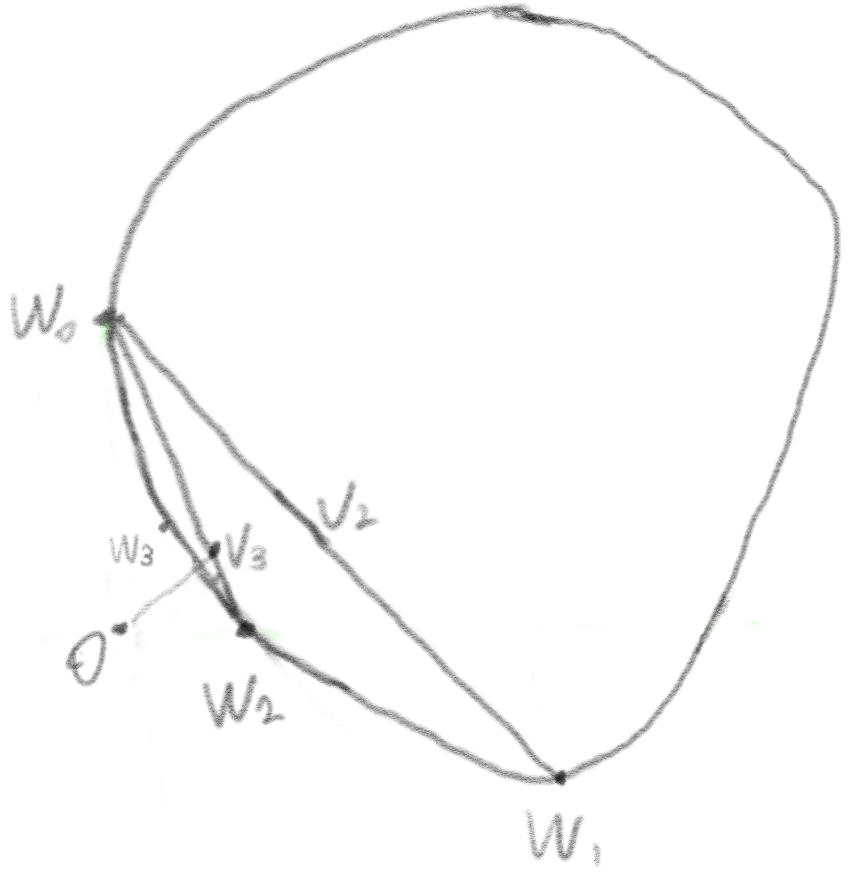
Find the closest point ![]() on the triangle (
on the triangle (![]() ,
, ![]() ,
, ![]() ). We can find the farthest point
). We can find the farthest point ![]() on the boundary along direction
on the boundary along direction ![]() . Now we focus on the new convex hull
. Now we focus on the new convex hull ![]() = <
= <![]() ,
, ![]() ,
, ![]() >.
>.
The length of the W triangle will become smaller as we continue these steps. For convex faceted objects, the closest point will be found in a finite number of steps.


