Here are three vectors ![]() (1, 0, 1),
(1, 0, 1), ![]() (-1, 0, 1) and
(-1, 0, 1) and ![]() (0, -1, 0) in the 3D world space.
(0, -1, 0) in the 3D world space.
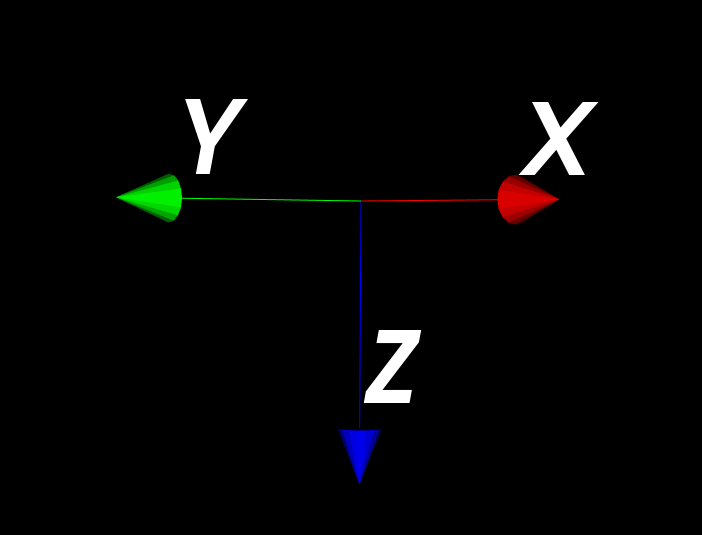
Define a position pos(1, 1, 0). These vector and position forms a new coordinate system A.
The inverse result is status B.
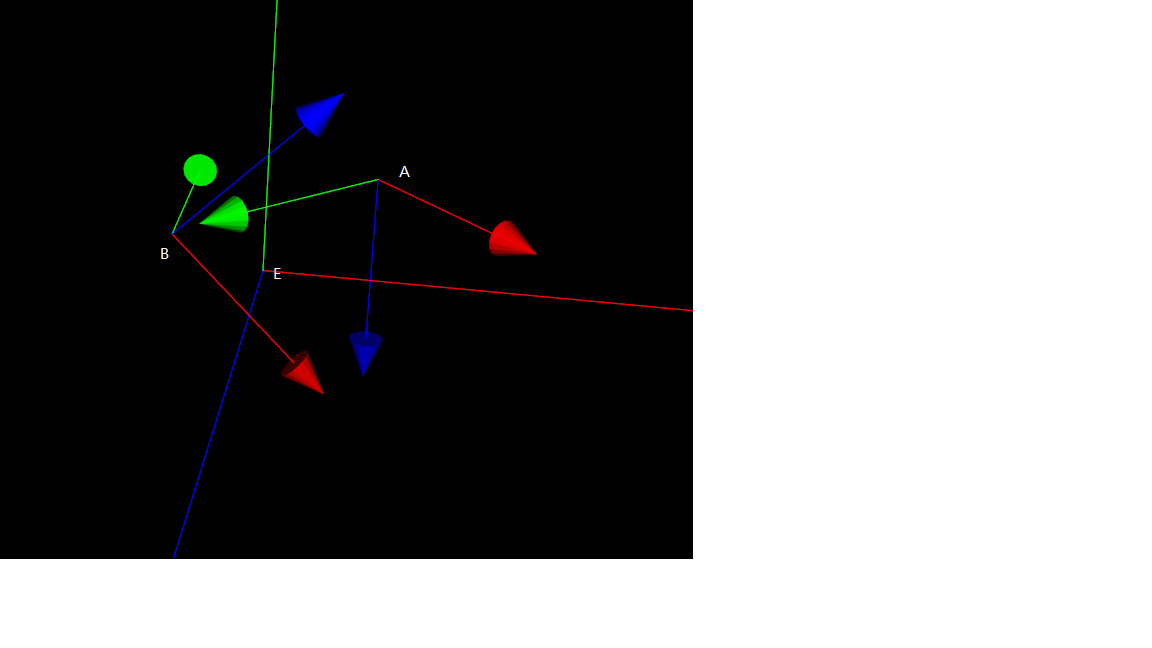
The original world coordinate system can be changed to A, the corresponding matrix is
![Rendered by QuickLaTeX.com \[M_1 = \begin{pmatrix} X_0 & Y_0 & Z_0 & P_0 \\ X_1 & Y_1 & Z_1 & P_1 \\ X_2 & Y_2 & Z_2 & P_2 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-e28fda8436ac9f7a794ed1048bd8c1fd_l3.png)
The original world coordinate system can be changed to B. We can explore it’s inverse matrix:
![Rendered by QuickLaTeX.com \[\begin{pmatrix} W_0 \\ W_1 \\ W_2 \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 & P_0 \\ 0 & 1 & 0 & P_1 \\ 0 & 0 & 1 & P_2 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} X_0 & Y_0 & Z_0 & 0 \\ X_1 & Y_1 & Z_1 & 0 \\ X_2 & Y_2 & Z_2 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} Q_0 \\ Q_1 \\ Q_2 \\ 1 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-66557da8d4705f0a742cb2902d70b2a0_l3.png)
![Rendered by QuickLaTeX.com \[\begin{pmatrix} Q_0 \\ Q_1 \\ Q_2 \\ 1 \end{pmatrix} = \begin{pmatrix} X_0 & X_1 & X_2 & 0 \\ Y_0 & Y_1 & Y_2 & 0 \\ Z_0 & Z_1 & Z_2 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & 0 & 0 & -P_0 \\ 0 & 1 & 0 & -P_1 \\ 0 & 0 & 1 & -P_2 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} W_0 \\ W_1 \\ W_2 \\ 1 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-1d516a141c783ce9914eda1008a0c935_l3.png)
So its inverse matrix is :
![Rendered by QuickLaTeX.com \[\begin{pmatrix} X_0 & X_1 & X_2 & 0 \\ Y_0 & Y_1 & Y_2 & 0 \\ Z_0 & Z_1 & Z_2 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix} \times \begin{pmatrix} 1 & 0 & 0 & -P_0 \\ 0 & 1 & 0 & -P_1 \\ 0 & 0 & 1 & -P_2 \\ 0 & 0 & 0 & 1 \end{pmatrix}\]](https://www.weiy.city/wp-content/ql-cache/quicklatex.com-7c3486f79206c360e4a60a85d7c75895_l3.png)
#include <iostream>
#include <vtkSmartPointer.h>
#include <vtkTransform.h>
#include <vtkActor.h>
#include <vtkConeSource.h>
#include <vtkRenderer.h>
#include <vtkRenderWindow.h>
#include <vtkPolyDataMapper.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkAxesActor.h>
#include <vtkLine.h>
#include <vtkPlane.h>
#include <vtkSphereSource.h>
#include "./point.hpp"
using namespace std;
#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();
int main()
{
Point xDir(1, 0, 1), yDir(-1, 0, 1), zDir(0, -1, 0), pos( 1, 1, 0 ); //pos(0, 0, 0);
xDir.Unit();
yDir.Unit();
zDir.Unit();
// pose trans: E => B
double elements1[16] = { xDir[0], yDir[0], zDir[0], pos[0],
xDir[1], yDir[1], zDir[1], pos[1],
xDir[2], yDir[2], zDir[2], pos[2],
0, 0, 0, 1 };
vtkSPtrNew( poseTrans, vtkTransform );
poseTrans->SetMatrix( elements1 );
poseTrans->Update();
poseTrans->PrintSelf( std::cout, vtkIndent() );
// local trans: E => A
double elements2[16] = { xDir[0], xDir[1], xDir[2], 0,
yDir[0], yDir[1], yDir[2], 0,
zDir[0], zDir[1], zDir[2], 0,
0, 0, 0, 1 };
vtkSPtrNew( localTrans, vtkTransform );
localTrans->SetMatrix( elements2 );
double elements3[16] = { 1, 0, 0, -pos[0],
0, 1, 0, -pos[1],
0, 0, 1, -pos[2],
0, 0, 0, 1 };
localTrans->Concatenate( elements3 );
localTrans->Update();
localTrans->PrintSelf( std::cout, vtkIndent() );
vtkSmartPointer<vtkAxesActor> axes0 = vtkSmartPointer<vtkAxesActor>::New();
axes0->SetTotalLength( 10, 10, 10 );
axes0->SetAxisLabels( false );
vtkSmartPointer<vtkAxesActor> axes1 = vtkSmartPointer<vtkAxesActor>::New();
axes1->SetTotalLength( 2, 2, 2 ); // change length of three axis
axes1->SetUserTransform( poseTrans );
axes1->SetAxisLabels( false );
vtkSmartPointer<vtkAxesActor> axes2 = vtkSmartPointer<vtkAxesActor>::New();
axes2->SetTotalLength( 2, 2, 2 ); // change length of three axis
axes2->SetUserTransform( localTrans );
axes2->SetAxisLabels( false );
vtkSPtrNew( renderer, vtkRenderer );
renderer->AddActor( axes0 );
renderer->AddActor( axes1 );
renderer->AddActor( axes2 );
renderer->SetBackground( 0, 0, 0 );
vtkSPtrNew( testTrans, vtkTransform ); //Concatenate( poseTrans ), Concatenate( localTrans ): pose x localTrans
testTrans->Concatenate( localTrans ); //Concatenate( localTrans ), Concatenate( poseTrans ): local x poseTrans
testTrans->Concatenate( poseTrans );
testTrans->Update();
testTrans->PrintSelf( std::cout, vtkIndent() );
/*
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
*/
vtkSPtrNew( renderWindow, vtkRenderWindow );
renderWindow->AddRenderer( renderer );
vtkSPtrNew( renderWindowInteractor, vtkRenderWindowInteractor );
renderWindowInteractor->SetRenderWindow( renderWindow );
renderer->ResetCamera();
renderWindow->Render();
renderWindowInteractor->Start();
return 0;
}
The order of rotations is opposite for the two processes.
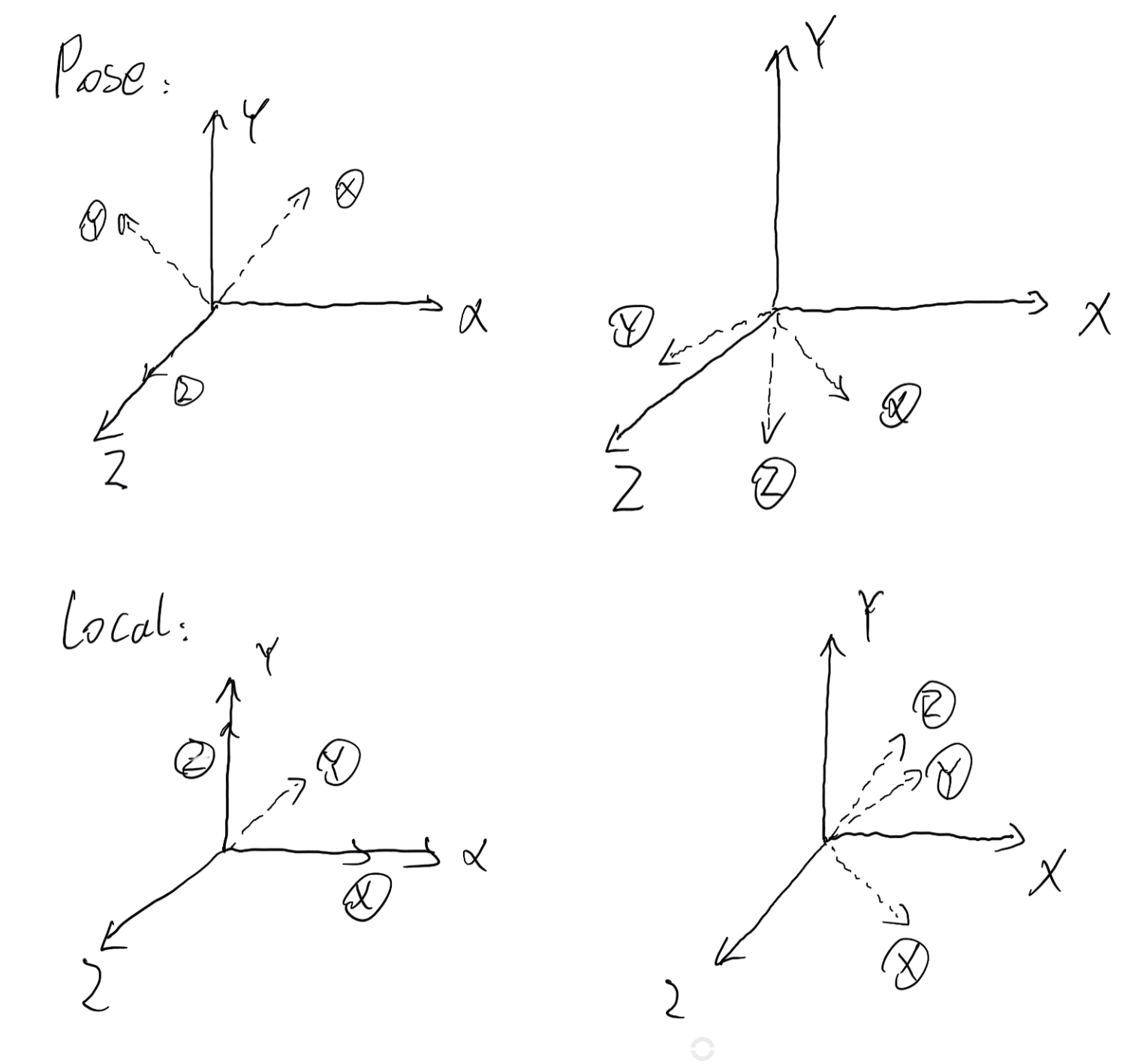


[…] Related post: https://www.weiy.city/2021/11/the-releationship-between-local-transform-and-pose-transform/ […]
[…] As we know, we can create a linear transform to change model to the special orientation and position. Refer to The Releationship Between Local Transform And Pose Transform. […]