Uniform Cubic Spline
Piecewise function:
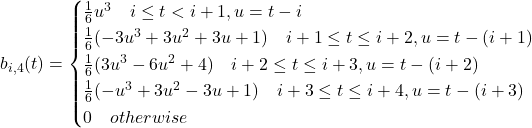
The cubic spline graph:
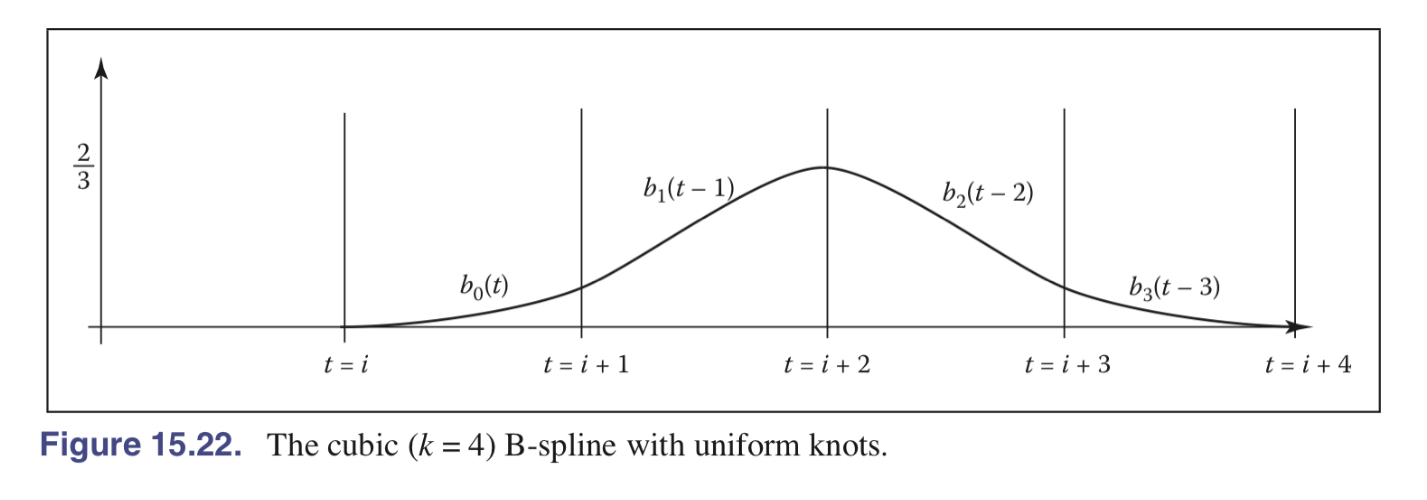
Test code:
#include <vtkActor.h>
#include <vtkCleanPolyData.h>
#include <vtkDistancePolyDataFilter.h>
#include <vtkNamedColors.h>
#include <vtkNew.h>
#include <vtkPointData.h>
#include <vtkPolyDataMapper.h>
#include <vtkPolyDataReader.h>
#include <vtkProperty.h>
#include <vtkRenderWindow.h>
#include <vtkRenderWindowInteractor.h>
#include <vtkRenderer.h>
#include <vtkScalarBarActor.h>
#include <vtkSmartPointer.h>
#include <vtkSphereSource.h>
#include <vtkSTLReader.h>
#include <vtkTransform.h>
#include <vtkMatrix4x4.h>
#include <vector>
#include <list>
#include "point.hpp"
#define vtkSPtr vtkSmartPointer
#define vtkSPtrNew(Var, Type) vtkSPtr<Type> Var = vtkSPtr<Type>::New();
std::vector<Point> originalPts = { Point(1, 0, 0), Point(3, 3, 0), Point(7, 5, 0), Point(9, 0, 0) };
vtkSmartPointer<vtkPolyData> ShowListByLine(std::vector<Point> list)
{
vtkSPtrNew( result, vtkPolyData );
vtkSPtrNew( resultPts, vtkPoints );
vtkSPtrNew( resultLines, vtkCellArray );
for( int i = 0; i < list.size(); ++i )
{
resultPts->InsertNextPoint( list[i].point );
}
for( int i = 0; i < list.size()-1; ++i )
{
vtkIdType pts[2] = { i, i + 1 };
resultLines->InsertNextCell( 2, pts );
}
result->SetPoints( resultPts );
result->SetLines( resultLines );
result->Modified();
return result;
}
int main(int argc, char* argv[])
{
double elements[16] = { -1, 3, -3, 1,
3, -6, 0, 4,
-3, 3, 3, 1,
1, 0, 0, 0};
vtkSmartPointer<vtkTransform> trans = vtkSmartPointer<vtkTransform>::New();
trans->SetMatrix( elements );
std::vector<Point> input2Pts;
auto getVarInVec = [](std::vector<Point> __originalPts, int index){
if(index >= __originalPts.size())
{
return __originalPts[__originalPts.size()-1]; //Point(0, 0, 0);
}
if(index < 0)
{
return __originalPts[0];
}
return __originalPts[index];
};
for( int i = -1; i < 3; ++i )
{
for(double u = 0; u < 1; u=u+0.1)
{
double vec[4] = { u*u*u, u*u, u, 1 };
double newVec[4];
trans->MultiplyPoint(vec, newVec);
Point newPt = (getVarInVec(originalPts, i+0)*newVec[0]+getVarInVec(originalPts, i+1)*newVec[1]+getVarInVec(originalPts, i+2)*newVec[2]+getVarInVec(originalPts, i+3)*newVec[3])*1/6.0;
input2Pts.push_back( newPt );
}
}
vtkSmartPointer<vtkPolyData> input1 = ShowListByLine( originalPts );
vtkSmartPointer<vtkPolyData> input2 = ShowListByLine( input2Pts );
vtkNew<vtkRenderWindow> renWin;
renWin->SetSize(1200, 500);
vtkNew<vtkRenderWindowInteractor> renWinInteractor;
renWinInteractor->SetRenderWindow(renWin);
double leftViewport[4] = {0.0, 0.0, 0.5, 1.0};
double rightViewport[4] = {0.5, 0.0, 1.0, 1.0};
vtkSPtrNew( mapper1, vtkPolyDataMapper );
mapper1->SetInputData( input1 );
vtkSPtrNew( actor1, vtkActor );
actor1->SetMapper( mapper1 );
vtkSPtrNew( mapper2, vtkPolyDataMapper );
mapper2->SetInputData( input2 );
vtkSPtrNew( actor2, vtkActor );
actor2->SetMapper( mapper2 );
// Setup renderers
vtkSPtrNew( leftRenderer, vtkRenderer );
leftRenderer->SetViewport( leftViewport );
leftRenderer->AddActor( actor1 );
leftRenderer->SetBackground(.6, .5, .4);
leftRenderer->ResetCamera();
vtkSPtrNew( rightRenderer, vtkRenderer );
rightRenderer->SetViewport(rightViewport);
rightRenderer->AddActor( actor2 );
rightRenderer->SetBackground(.4, .5, .6);
rightRenderer->SetActiveCamera( leftRenderer->GetActiveCamera() );
renWin->AddRenderer( leftRenderer );
renWin->AddRenderer( rightRenderer );
renWin->Render();
renWinInteractor->Start();
return EXIT_SUCCESS;
}
Result:

Uniform Quadratic Spline
Basis Piecewise function:
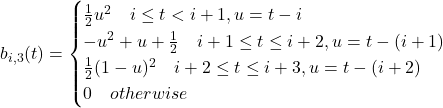
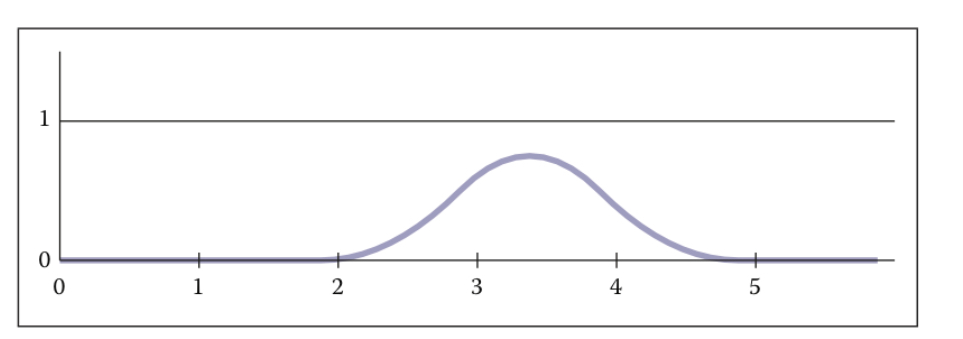
Implementation:
std::vector<Point> input2Pts;
auto getVarInVec = [](std::vector<Point> __originalPts, int index){
if(index >= __originalPts.size())
{
return __originalPts[__originalPts.size()-1]; //Point(0, 0, 0);
}
if(index < 0)
{
return __originalPts[0];
}
return __originalPts[index];
};
for( int i = -1; i < 3; ++i )
{
for(double u = 0; u < 1; u=u+0.1)
{
double vec[3] = { (1-u)*(1-u)*0.5, -u*u+u+0.5, u*u*0.5 };
Point newPt = getVarInVec(originalPts, i+0)*vec[0]+getVarInVec(originalPts, i+1)*vec[1]+getVarInVec(originalPts, i+2)*vec[2];
input2Pts.push_back( newPt );
}
}

Uniform Linear Spline
Basis functions:
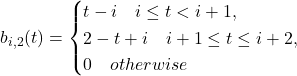
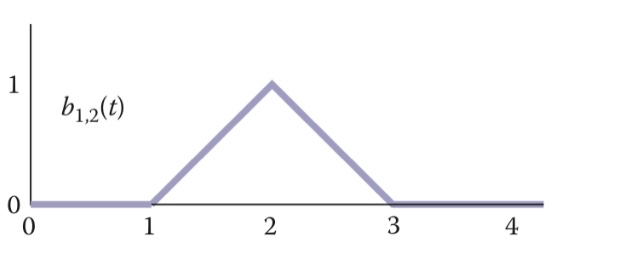
Test code:
std::vector<Point> input2Pts;
auto getVarInVec = [](std::vector<Point> __originalPts, int index){
if(index >= __originalPts.size())
{
return __originalPts[__originalPts.size()-1]; //Point(0, 0, 0);
}
if(index < 0)
{
return __originalPts[0];
}
return __originalPts[index];
};
for( int i = 0; i < 4; ++i )
{
for(double u = 0; u < 1; u=u+0.3)
{
double vec[2] = { 1-u, u };
Point newPt = getVarInVec(originalPts, i+0)*vec[0]+getVarInVec(originalPts, i+1)*vec[1];
input2Pts.push_back( newPt );
std::cout << "newPt: " << newPt[0] << ", " << newPt[1] << ", " << newPt[2] << std::endl;
}
}
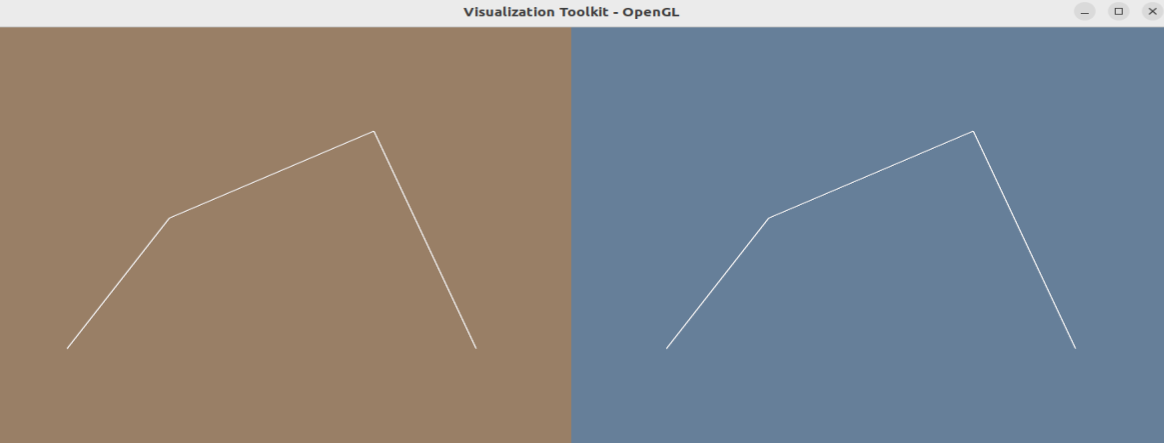


[…] input points and use the Cubic piecewise function introduced in Basic functions for B-Spline to create smooth […]