Here is a convex object and an origin point outside it.
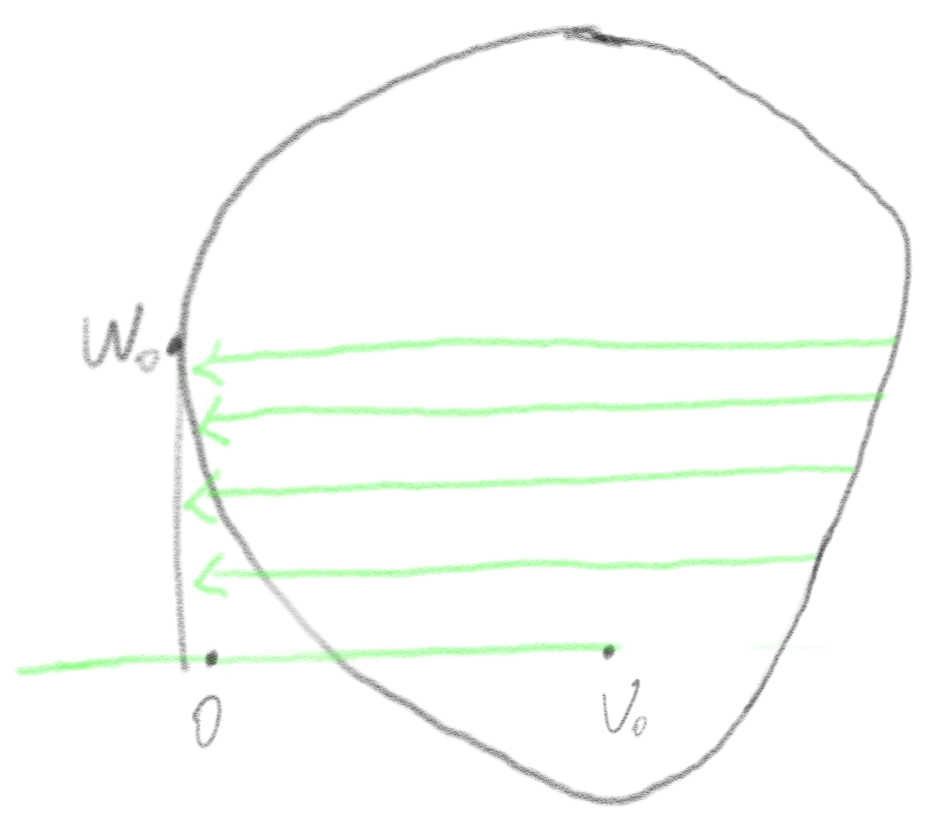
is an arbitrary point in the boundary. Find the farthest point on the boundary along the vector 
. Name the farthest point 
.
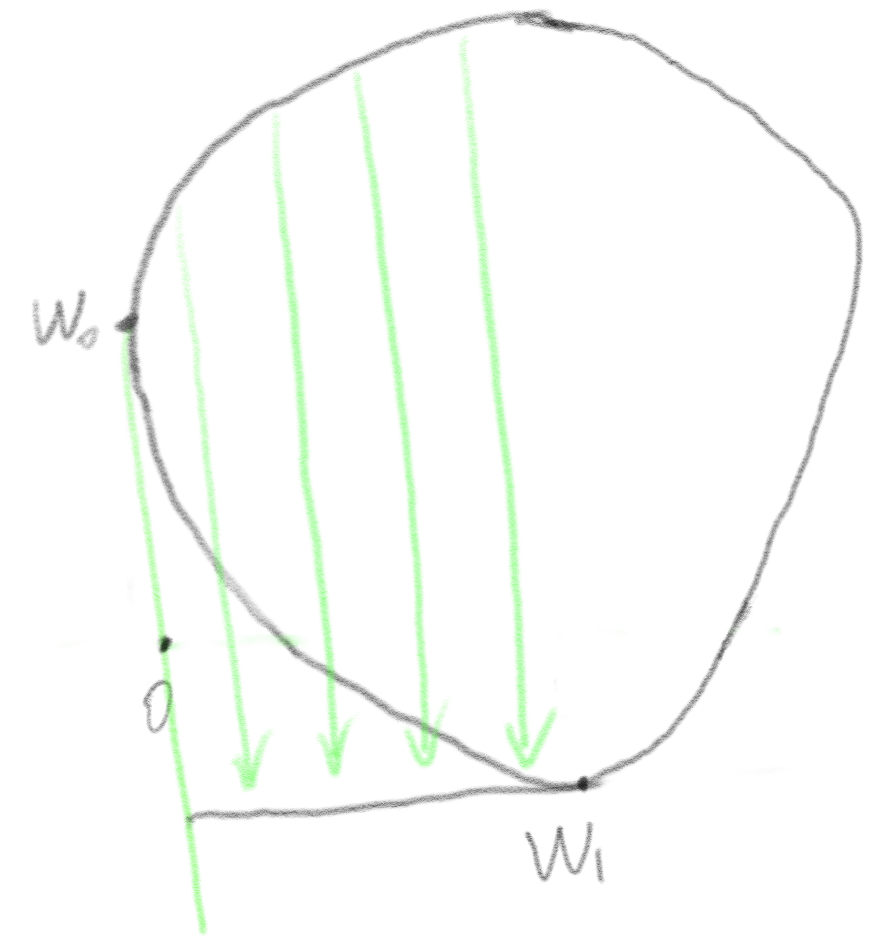
We get a new vector 
to find the farthest point on the boundary along the direction . The point 
is added to the simple vertices set 
= {, }.
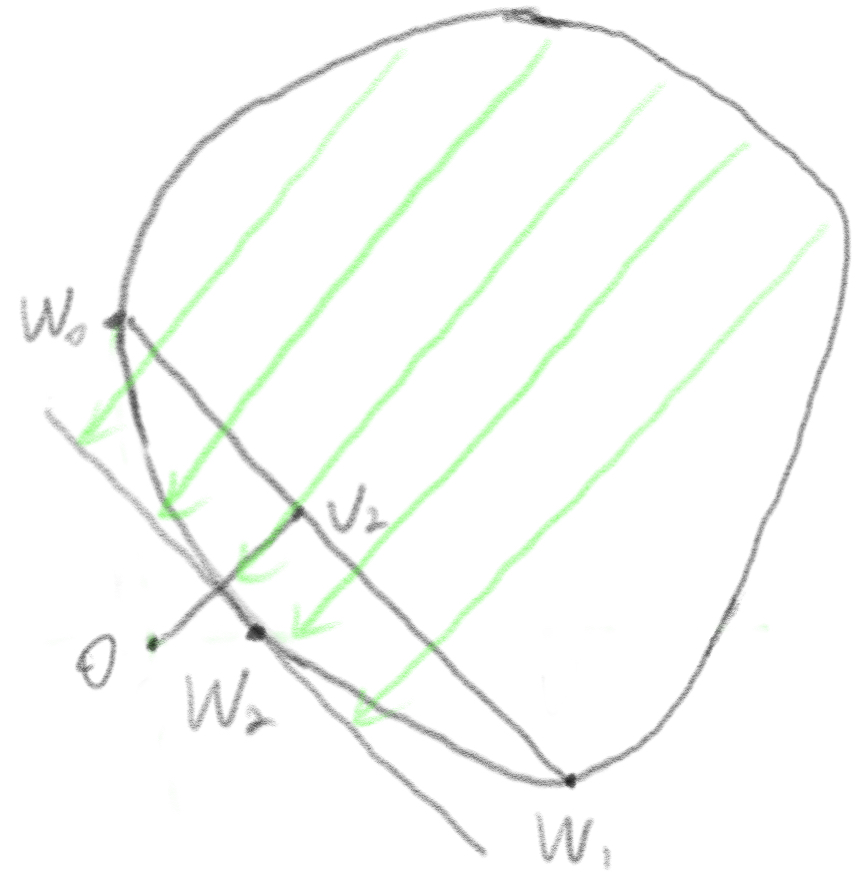
Connect points and , find the closet point 
on the line segment to the origin O. Find the farthest point 
on the boundary with direction 
. The point is added to the simple vertices set 
= {, , }.
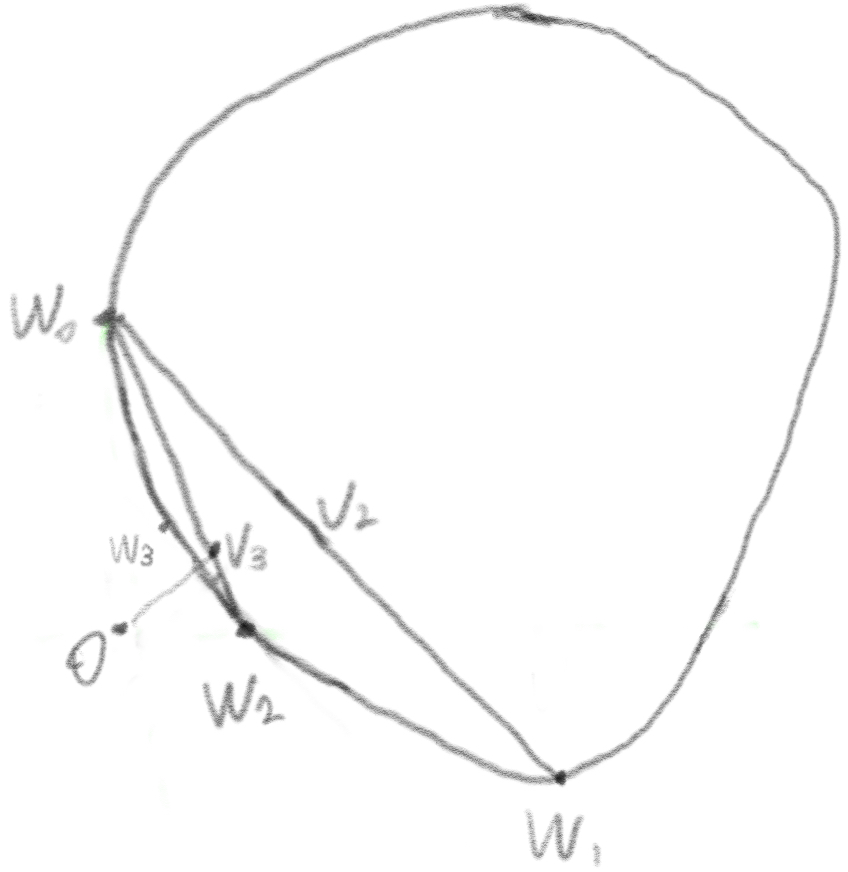
Find the closest point 
on the triangle (, , ). We can find the farthest point 
on the boundary along direction 
. Now we focus on the new convex hull 
= <, , >.
The length of the W triangle will become smaller as we continue these steps. For convex faceted objects, the closest point will be found in a finite number of steps.
